十二面体的纽结怎么画
十二面体的纽结怎么画
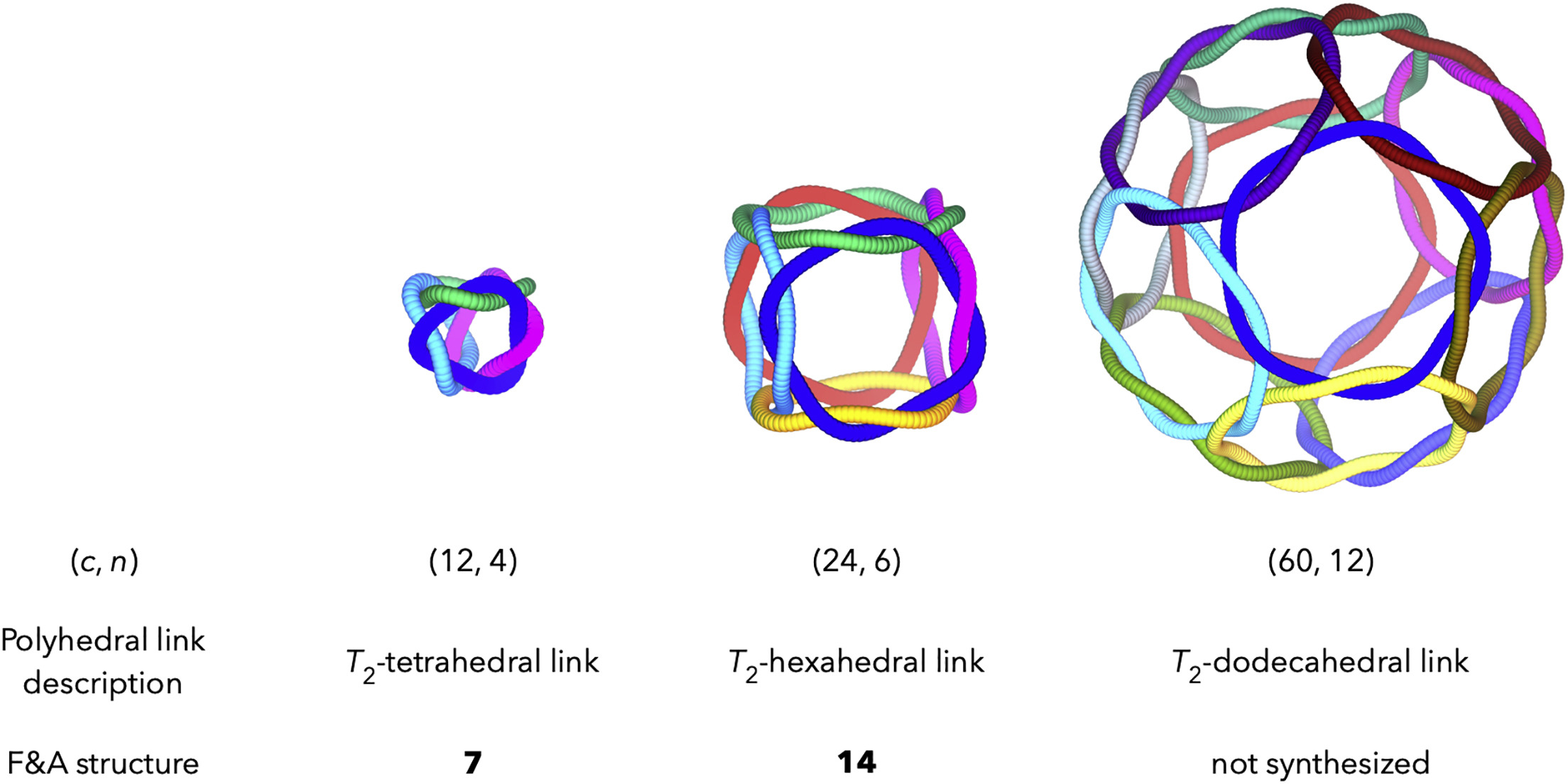
绘制思路
- 绘制正十二面体
- 找到每条边的特征点,创建顺时针绕过边的折线。
- 遍历并绘制平滑插值后的折线(下列代码按面遍历,请注意每条边需要遍历两次)
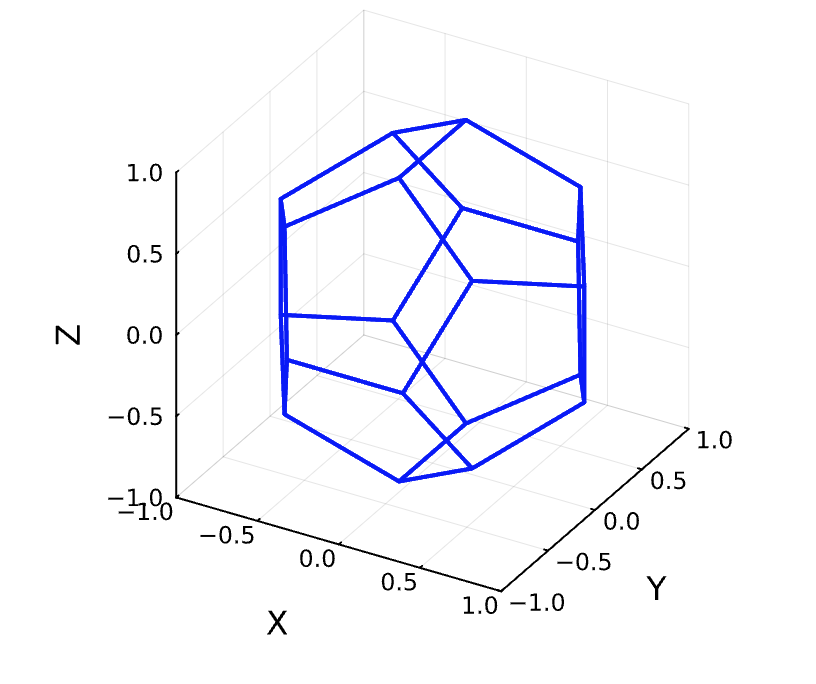
Julia 代码
展开
Julia
# Wang Zilong @ ciac <ZilongWang@mail.ustc.edu.cn> 2025.02.21
# Julia version
using Plots
using LinearAlgebra
using Interpolations
# 正十二面体的面数据 (已提供)
dodeca = [
[
-0.5773503 0.5773503 0.5773503
0.0 0.3567822 0.9341724
0.0 -0.3567822 0.9341724
-0.5773503 -0.5773503 0.5773503
-0.9341724 0.0 0.3567822
],
[
0.5773503 -0.5773503 0.5773503
0.3567822 -0.9341724 0.0
-0.3567822 -0.9341724 0.0
-0.5773503 -0.5773503 0.5773503
0.0 -0.3567822 0.9341724
],
[
-0.5773503 -0.5773503 0.5773503
-0.3567822 -0.9341724 0.0
-0.5773503 -0.5773503 -0.5773503
-0.9341724 0.0 -0.3567822
-0.9341724 0.0 0.3567822
],
[
-0.9341724 0.0 0.3567822
-0.9341724 0.0 -0.3567822
-0.5773503 0.5773503 -0.5773503
-0.3567822 0.9341724 0.0
-0.5773503 0.5773503 0.5773503
],
[
0.0 0.3567822 0.9341724
-0.5773503 0.5773503 0.5773503
-0.3567822 0.9341724 0.0
0.3567822 0.9341724 0.0
0.5773503 0.5773503 0.5773503
],
[
0.0 -0.3567822 0.9341724
0.0 0.3567822 0.9341724
0.5773503 0.5773503 0.5773503
0.9341724 0.0 0.3567822
0.5773503 -0.5773503 0.5773503
],
[
0.5773503 0.5773503 -0.5773503
0.9341724 0.0 -0.3567822
0.5773503 -0.5773503 -0.5773503
0.0 -0.3567822 -0.9341724
0.0 0.3567822 -0.9341724
],
[
0.5773503 -0.5773503 -0.5773503
0.0 -0.3567822 -0.9341724
-0.5773503 -0.5773503 -0.5773503
-0.3567822 -0.9341724 0.0
0.3567822 -0.9341724 0.0
],
[
-0.5773503 0.5773503 -0.5773503
-0.9341724 0.0 -0.3567822
-0.5773503 -0.5773503 -0.5773503
0.0 -0.3567822 -0.9341724
0.0 0.3567822 -0.9341724
],
[
-0.5773503 0.5773503 -0.5773503
0.0 0.3567822 -0.9341724
0.5773503 0.5773503 -0.5773503
0.3567822 0.9341724 0.0
-0.3567822 0.9341724 0.0
],
[
0.5773503 0.5773503 0.5773503
0.3567822 0.9341724 0.0
0.5773503 0.5773503 -0.5773503
0.9341724 0.0 -0.3567822
0.9341724 0.0 0.3567822
],
[
0.5773503 -0.5773503 0.5773503
0.9341724 0.0 0.3567822
0.9341724 0.0 -0.3567822
0.5773503 -0.5773503 -0.5773503
0.3567822 -0.9341724 0.0
],
]
tetra = [
# 面1
[
0.0 0.0 1.0
0.9428090415820634 0.0 -0.3333333333333333
-0.4714045207910317 0.8164965809277259 -0.3333333333333333
],
# 面2
[
0.0 0.0 1.0
-0.4714045207910317 0.8164965809277259 -0.3333333333333333
-0.4714045207910317 -0.8164965809277259 -0.3333333333333333
],
# 面3
[
0.0 0.0 1.0;
-0.4714045207910317 -0.8164965809277259 -0.3333333333333333
0.9428090415820634 0.0 -0.3333333333333333
],
# 面4
[
0.9428090415820634 0.0 -0.3333333333333333
-0.4714045207910317 -0.8164965809277259 -0.3333333333333333
-0.4714045207910317 0.8164965809277259 -0.3333333333333333
]
]
# 计算三等分点和中点
function get_points(v1, v2)
midpoint = (v1 + v2) / 2
third1 = v1 + (v2 - v1) / 3
third2 = v1 + 2 * (v2 - v1) / 3
return midpoint, third1, third2
end
# 计算面心和体心
function calculate_centers(face)
face_center = sum(face, dims=1) / size(face, 1)
body_center = [0.0, 0.0, 0.0] # 体心为原点
return face_center[:], body_center
end
# 创建平滑的插值曲线
function interpolate_curve(points)
if length(points) < 3
error("At least 3 points are required for interpolation.")
end
points_matrix = hcat(points...)'
t = 1:size(points_matrix, 1)
itp_x = cubic_spline_interpolation(t, points_matrix[:, 1])
itp_y = cubic_spline_interpolation(t, points_matrix[:, 2])
itp_z = cubic_spline_interpolation(t, points_matrix[:, 3])
t_smooth = range(1, size(points_matrix, 1), length=100)
x_smooth = itp_x.(t_smooth)
y_smooth = itp_y.(t_smooth)
z_smooth = itp_z.(t_smooth)
return hcat(x_smooth, y_smooth, z_smooth)
end
function sort_face_vertices!(face, face_center)
normal = -face_center # 近似法向量:面心指向体心
# 找到一个与法向量不平行的向量 (例如 [1, 0, 0])
arbitrary_vector = [1.0, 0.0, 0.0]
if abs(dot(normal, arbitrary_vector)) > 0.99 # 如果太接近平行,换一个向量
arbitrary_vector = [0.0, 1.0, 0.0]
end
u = normalize(cross(normal, arbitrary_vector)) # 第一个基向量
v = normalize(cross(normal, u)) # 第二个基向量,与 u 和 normal 都正交
angles = []
for vertex in eachrow(face)
vec_to_vertex = vertex - face_center
x_proj = dot(vec_to_vertex, u)
y_proj = dot(vec_to_vertex, v)
angle = atan(y_proj, x_proj) # 计算角度
push!(angles, angle)
end
# 获取排序后的索引 (顺时针 - 角度递减排序)
sorted_indices = sortperm(angles, rev=true) # rev=true for clockwise, 可以尝试 rev=false for counter-clockwise
# 根据排序后的索引重新排列顶点
face[:] = face[sorted_indices, :] # 使用 [:] 来原地修改 face 的内容
end
# Sort vertices for each face in dodeca
for i in eachindex(dodeca)
face_center, _ = calculate_centers(dodeca[i])
sort_face_vertices!(dodeca[i], face_center)
end
for i in eachindex(tetra)
face_center, _ = calculate_centers(tetra[i])
sort_face_vertices!(tetra[i], face_center)
end
# --- Modified Plotting Section ---
# Choose a backend (try these one at a time)
# gr()
plotlyjs()
# pgfplotsx()
# Create 3D plot with some initial viewing angle
plot3d(
1,
xlim = (-1.1, 1.1),
ylim = (-1.1, 1.1),
zlim = (-1.1, 1.1),
aspect_ratio = :equal,
legend = false,
xlabel = "X",
ylabel = "Y",
zlabel = "Z",
title = "Dodecahedron with Smooth Inner Curves (Sorted Vertices)",
camera = (30, 60) # Set initial camera angle (azimuth, elevation)
)
# # 绘制正十二面体的边 (same as before)
# for face in dodeca
# x = face[:, 1]
# y = face[:, 2]
# z = face[:, 3]
# x = [x; x[1]; NaN]
# y = [y; y[1]; NaN]
# z = [z; z[1]; NaN]
# plot!(x, y, z, linecolor = :blue, linewidth = 2)
# end
# 绘制内部曲线 (same as before)
for (l,face) in enumerate(dodeca) # dodeca tetra
face_center, body_center = calculate_centers(face)
num_vertices = size(face, 1)
color = [:red, :green, :blue, :orange, :purple, :cyan, :magenta, :yellow, :brown, :pink, :gray, :black]
lines2Plot = []
for i in 1:num_vertices
v1 = face[i, :]
v2 = face[mod(i, num_vertices) + 1, :]
midpoint, third1, third2 = get_points(v1, v2)
p1 = v1 + 0.2 * (face_center - v1)
p2 = third1 + 0.1 * (body_center - third1) # Corrected: towards body center
p3 = midpoint - 0.1 * (face_center - midpoint)
p4 = third2 - 0.1 * (body_center - third2) # Corrected: away from body center
p5 = v2 + 0.2 * (face_center - v2)
curve1 = interpolate_curve([p1, p2, p3, p4, p5])
plot!(curve1[:, 1], curve1[:, 2], curve1[:, 3], linecolor = color[l], linewidth = 7)
# append!(lines2Plot, [p1, p2, p3, p4, p5])
end
# curve1 = interpolate_curve(lines2Plot)
# plot!(curve1[:, 1], curve1[:, 2], curve1[:, 3], linecolor = color[l], linewidth = 15)
end
display(plot!())Python 代码
展开
Python
# Wang Zilong @ ciac <ZilongWang@mail.ustc.edu.cn> 2025.02.21
# Python version
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.interpolate import CubicSpline
# tetra = [
# # 面1
# [
# 0.0 0.0 1.0
# 0.9428090415820634 0.0 -0.3333333333333333
# -0.4714045207910317 0.8164965809277259 -0.3333333333333333
# ],
# # 面2
# [
# 0.0 0.0 1.0
# -0.4714045207910317 0.8164965809277259 -0.3333333333333333
# -0.4714045207910317 -0.8164965809277259 -0.3333333333333333
# ],
# # 面3
# [
# 0.0 0.0 1.0;
# -0.4714045207910317 -0.8164965809277259 -0.3333333333333333
# 0.9428090415820634 0.0 -0.3333333333333333
# ],
# # 面4
# [
# 0.9428090415820634 0.0 -0.3333333333333333
# -0.4714045207910317 -0.8164965809277259 -0.3333333333333333
# -0.4714045207910317 0.8164965809277259 -0.3333333333333333
# ]
# ]
tetra = [
np.array([
[0.0, 0.0, 1.0],
[0.9428090415820634, 0.0, -0.3333333333333333],
[-0.4714045207910317, 0.8164965809277259, -0.3333333333333333],
]),
np.array([
[0.0, 0.0, 1.0],
[-0.4714045207910317, 0.8164965809277259, -0.3333333333333333],
[-0.4714045207910317, -0.8164965809277259, -0.3333333333333333],
]),
np.array([
[0.0, 0.0, 1.0],
[-0.4714045207910317, -0.8164965809277259, -0.3333333333333333],
[0.9428090415820634, 0.0, -0.3333333333333333],
]),
np.array([
[0.9428090415820634, 0.0, -0.3333333333333333],
[-0.4714045207910317, -0.8164965809277259, -0.3333333333333333],
[-0.4714045207910317, 0.8164965809277259, -0.3333333333333333],
]),
]
# 正十二面体的面数据 (已提供)
dodeca = [
np.array([
[-0.5773503, 0.5773503, 0.5773503],
[ 0.0, 0.3567822, 0.9341724],
[ 0.0, -0.3567822, 0.9341724],
[-0.5773503, -0.5773503, 0.5773503],
[-0.9341724, 0.0, 0.3567822],
]),
np.array([
[ 0.5773503, -0.5773503, 0.5773503],
[ 0.3567822, -0.9341724, 0.0],
[-0.3567822, -0.9341724, 0.0],
[-0.5773503, -0.5773503, 0.5773503],
[ 0.0, -0.3567822, 0.9341724],
]),
np.array([
[-0.5773503, -0.5773503, 0.5773503],
[-0.3567822, -0.9341724, 0.0],
[-0.5773503, -0.5773503, -0.5773503],
[-0.9341724, 0.0, -0.3567822],
[-0.9341724, 0.0, 0.3567822],
]),
np.array([
[-0.9341724, 0.0, 0.3567822],
[-0.9341724, 0.0, -0.3567822],
[-0.5773503, 0.5773503, -0.5773503],
[-0.3567822, 0.9341724, 0.0],
[-0.5773503, 0.5773503, 0.5773503],
]),
np.array([
[ 0.0, 0.3567822, 0.9341724],
[-0.5773503, 0.5773503, 0.5773503],
[-0.3567822, 0.9341724, 0.0],
[ 0.3567822, 0.9341724, 0.0],
[ 0.5773503, 0.5773503, 0.5773503],
]),
np.array([
[ 0.0, -0.3567822, 0.9341724],
[ 0.0, 0.3567822, 0.9341724],
[ 0.5773503, 0.5773503, 0.5773503],
[ 0.9341724, 0.0, 0.3567822],
[ 0.5773503, -0.5773503, 0.5773503],
]),
np.array([
[ 0.5773503, 0.5773503, -0.5773503],
[ 0.9341724, 0.0, -0.3567822],
[ 0.5773503, -0.5773503, -0.5773503],
[ 0.0, -0.3567822, -0.9341724],
[ 0.0, 0.3567822, -0.9341724],
]),
np.array([
[ 0.5773503, -0.5773503, -0.5773503],
[ 0.0, -0.3567822, -0.9341724],
[-0.5773503, -0.5773503, -0.5773503],
[-0.3567822, -0.9341724, 0.0],
[ 0.3567822, -0.9341724, 0.0],
]),
np.array([
[-0.5773503, 0.5773503, -0.5773503],
[-0.9341724, 0.0, -0.3567822],
[-0.5773503, -0.5773503, -0.5773503],
[ 0.0, -0.3567822, -0.9341724],
[ 0.0, 0.3567822, -0.9341724],
]),
np.array([
[-0.5773503, 0.5773503, -0.5773503],
[ 0.0, 0.3567822, -0.9341724],
[ 0.5773503, 0.5773503, -0.5773503],
[ 0.3567822, 0.9341724, 0.0],
[-0.3567822, 0.9341724, 0.0],
]),
np.array([
[ 0.5773503, 0.5773503, 0.5773503],
[ 0.3567822, 0.9341724, 0.0],
[ 0.5773503, 0.5773503, -0.5773503],
[ 0.9341724, 0.0, -0.3567822],
[ 0.9341724, 0.0, 0.3567822],
]),
np.array([
[ 0.5773503, -0.5773503, 0.5773503],
[ 0.9341724, 0.0, 0.3567822],
[ 0.9341724, 0.0, -0.3567822],
[ 0.5773503, -0.5773503, -0.5773503],
[ 0.3567822, -0.9341724, 0.0],
]),
]
# 计算三等分点和中点
def get_points(v1, v2):
midpoint = (v1 + v2) / 2
third1 = v1 + (v2 - v1) / 3
third2 = v1 + 2 * (v2 - v1) / 3
return midpoint, third1, third2
# 计算面心和体心
def calculate_centers(face):
face_center = np.mean(face, axis=0)
body_center = np.array([0.0, 0.0, 0.0]) # 体心为原点
return face_center, body_center
# 创建平滑的插值曲线
def interpolate_curve(points):
if len(points) < 3:
raise ValueError("At least 3 points are required for interpolation.")
points_matrix = np.array(points)
t = np.arange(len(points_matrix))
# 使用CubicSpline进行插值
cs_x = CubicSpline(t, points_matrix[:, 0])
cs_y = CubicSpline(t, points_matrix[:, 1])
cs_z = CubicSpline(t, points_matrix[:, 2])
t_smooth = np.linspace(t[0], t[-1], 100)
x_smooth = cs_x(t_smooth)
y_smooth = cs_y(t_smooth)
z_smooth = cs_z(t_smooth)
return np.vstack((x_smooth, y_smooth, z_smooth)).T
# 排序顶点
def sort_face_vertices(face, face_center):
normal = -face_center # 近似法向量:面心指向体心
arbitrary_vector = np.array([1.0, 0.0, 0.0])
if np.abs(np.dot(normal, arbitrary_vector)) > 0.99:
arbitrary_vector = np.array([0.0, 1.0, 0.0])
u = np.cross(normal, arbitrary_vector)
u = u / np.linalg.norm(u)
v = np.cross(normal, u)
v = v / np.linalg.norm(v)
angles = []
for vertex in face:
vec_to_vertex = vertex - face_center
x_proj = np.dot(vec_to_vertex, u)
y_proj = np.dot(vec_to_vertex, v)
angle = np.arctan2(y_proj, x_proj)
angles.append(angle)
sorted_indices = np.argsort(angles)[::-1] # 顺时针排序
return face[sorted_indices]
# Sort vertices for each face in dodeca
for i in range(len(dodeca)):
face_center, _ = calculate_centers(dodeca[i])
dodeca[i] = sort_face_vertices(dodeca[i], face_center)
# 绘制正十二面体的边和内部曲线
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlim(-1.1, 1.1)
ax.set_ylim(-1.1, 1.1)
ax.set_zlim(-1.1, 1.1)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Dodecahedron with Smooth Inner Curves (Sorted Vertices)')
# color = [:red, :green, :blue, :orange, :purple, :cyan, :magenta, :yellow, :brown, :pink, :gray, :black]
color = ['red', 'green', 'blue', 'orange', 'purple', 'cyan', 'magenta', 'yellow', 'brown', 'pink', 'gray', 'black']
# tetra dodeca
for face, c in zip(tetra, color):
face_center, body_center = calculate_centers(face)
num_vertices = len(face)
for i in range(num_vertices):
v1 = face[i]
v2 = face[(i + 1) % num_vertices]
midpoint, third1, third2 = get_points(v1, v2)
p1 = v1 + 0.2 * (face_center - v1)
p2 = third1 + 0.05 * (body_center - third1)
p3 = midpoint - 0.05 * (face_center - midpoint)
p4 = third2 - 0.05 * (body_center - third2)
p5 = v2 + 0.2 * (face_center - v2)
curve1 = interpolate_curve([p1, p2, p3, p4, p5])
ax.plot(curve1[:, 0], curve1[:, 1], curve1[:, 2], color=c, linewidth=2)
plt.show()ps: 网上找到了这个 https://www.math.utoronto.ca/graduate/pce/algebra/Alg-1994Jan.pdf